안녕하세요, '7급 PSAT에 최적화되다!’ 메가피셋입니다. 오늘은 ‘PSAT 진단과 맞춤전략’ 두 번 째 회차인 자료해석 편인데요, 메가피셋 대표강사 김승환 교수님께서 수험생 분들을 위해 직접 한 땀 한 땀 그래픽 작업까지 하시며 “하면 오르는 자료해석” 공부법을 소개해주셨습니다.

1) 자료해석 반드시 정확하게 계산해야 할까?
안녕하세요 여러분, 김승환입니다. PSAT 자료해석 공부를 시작할 때 많은 수험생 분들이 어려움을 겪는 영역이 바로 ‘계산’과 관련된 부분입니다. 그동안 계산이 어느 정도로 필요한지 시원하게 해답을 주는 사람이 없었기 때문에 ‘무조건 계산을 피하려고 하거나’, 반대로 ‘언제나 정확한 계산을 통해 해결’하려 하는 경우가 많았습니다. 안타깝게도 이는 자료해석에 대한 오해에서 비롯된 왜곡된 접근법으로서 수험생활에 있어 쓰디 쓴 시행착오가 발생할 수 있습니다.
저는 자료해석을 ‘자료를 해석하는 능력과 해석에 필요한 값을 도출·추론 하는 능력을 측정하는 시험’으로 정의합니다. 따라서 불필요한 계산을 피할 수 있도록 아이디어와 구조의 해석 기법을 전달 드리면서도 필요한 계산을 가볍고 효율적으로 처리할 수 있는 강력한 스킬들과 사고 노하우들을 전달드립니다. 이는 그간 수강생분들께 큰 성과가 있었습니다.
다음 실제 기출 문제의 <보기 ㄱ>을 함께 풀어보며 생각해 보도록 하겠습니다.
문 1. 다음 <표>와 <그림>은 A지역 2016년 주요 버섯의 도․소매가와 주요 버섯 소매가의 전년 동분기 대비 등락액을 나타낸 자료이다. 이에 대한 <보기>의 설명 중 옳은 것만을 모두 고르면?
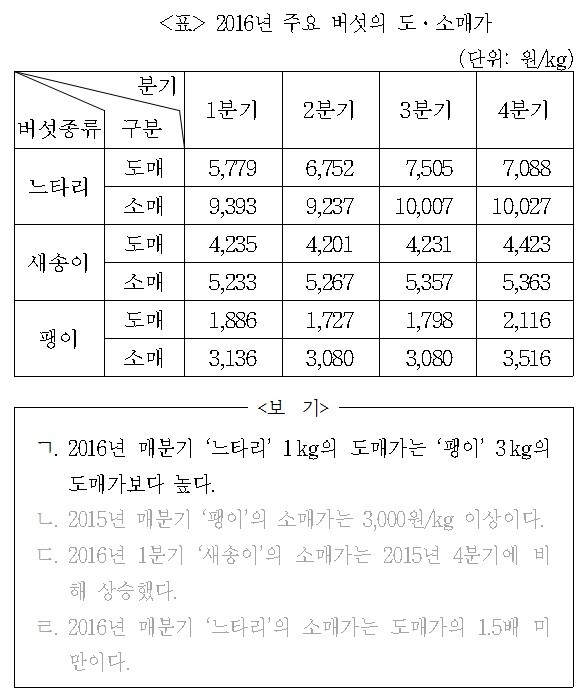
<보기> ㄱ은 ‘느타리’ 1kg의 도매가가 매분기 ‘팽이’ 3kg의 도매가보다 높은지를 묻고 있습니다. 주어진 <표>는 버섯 종류별 1kg당 도매가를 의미하기 때문에 선지의 정오를 판단하기 위해 <표>에 주어진 ‘팽이 도매가의 3배’를 계산하여 ‘느타리 도매가’와 비교하는 판단을 ‘1분기∼4분기’까지 4번 해야 합니다.
즉, 1분기의 경우 ‘느타리 도매가(5,779)’가 ‘팽이 도매가(1,886)×3’보다 더 큰지를 판단해야 합니다. 마찬가지로 2분기는 ‘6,752>1,727×3’인지, 3분기는 ‘7,505>1,798×3’인지, 4분기는 ‘7,088>2,116×3’인지를 확인해야 합니다. 물론 이 계산을 정확하게 해야 한다면 그것은 몹시 괴로운 일이 아닐 수 없습니다.
이때 제가 전달 드리는 저의 사고 기술(Skill)인 ‘크게 보기’ 기법이 간편하고 빠른 판단을 위해 큰 도움이 됩니다. ‘크게 보기’란 계산에 활용되는 숫자를 조금 크게 보아 계산하기 간편한 숫자를 활용하여 빠르고 간편하게 계산을 처리하는 기법을 의미합니다. 이를 활용하여 1분기부터 ‘크게 보기’를 활용하여 함께 해결 해보도록 합시다.
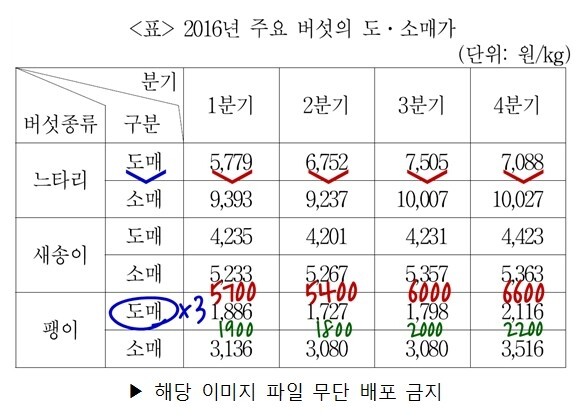
‘5,779>1,886×3’을 확인할 때 1,886의 3배에서 계산하기 까다로운 1,886을 1,900으로 크게 보아 3배를 생각하면 5,700이 됩니다. 이는 팽이의 도매가의 3배를 크게 보아 5,700으로 보더라도 느타리의 도매가(5,779)가 더 큼을 의미합니다. 따라서 크게 보기 전의 팽이 도매가 1,886의 3배 보다 5,779가 클 것임을 쉽게 알 수 있습니다.
마찬가지 방법으로 2분기 ‘6,752(느타리)>1,727(팽이)×3’의 우변은 1,727을 1,800으로 크게 보아도 5,400이 되어 느타리가 더 크다는 사실을 쉽게 알 수 있고, 3분기는 ‘7,505(느타리)>1,798(팽이)×3’의 우변은 1,798을 2,000으로 크게 보더라도 6,000이 되어 느타리가 더 크다는 것을 쉽게 확인 가능하며, 4분기 역시 ‘7,088(느타리)>2,116(팽이)×3’은 2,116을 2,200으로 크게 보아도 6,600이 되어 느타리가 더 큼을 쉽게 알 수 있습니다. 따라서 모든 분기가 느타리가 더 크기 때문에 옳은 선지가 됩니다.
만약 이 문제를 해결하며 3배를 일일이 정확하게 계산하려 했다면 시간도 오래 걸리고 불필요한 체력을 낭비하게 되었을 것입니다. 반대로 ‘크게 보기’ 기술이 훈련되어 있었다면 ㄱ선지를 맞다고 판단하는 순간 선지 ③,④,⑤가 한꺼번에 소거되기 때문에 추가적으로 선지 하나만 보고 간단하게 정답 도출이 가능했던 문제였습니다. 자료해석은 이처럼 빠르고 효율적인 계산 노하우들을 학습하교 훈련함으로써 언제나 정확한 계산을 하는 것이 아니라 계산을 보다 간편하고 효율적으로 처리하여 문제 풀이 속도를 높여갈 수 있습니다.
2) 그렇다면 계산이 필요한 문제와 그렇지 않은 문제를 구별하는 방법은?
앞선 예제처럼 PSAT 자료해석에서 계산의 효율적 처리 능력은 매우 중요한 부분입니다. 실전에서는 계산을 해야 할 때와 계산 없이 해석 처리 할 때를 순간순간 구분할 수 있는 힘이 매우 중요하다는 것이 저의 신념입니다. 다음 실제 기출 문제에서 <보기> ㄱ을 우선 해결해 보시길 바랍니다.
문 2. 다음 <표>는 2014~2018년 ‘갑’국의 전력단가와 에너지원별 평균정산단가에 관한 자료이다. 이에 대한 <보기>의 설명 중 옳은 것만을 모두 고르면?
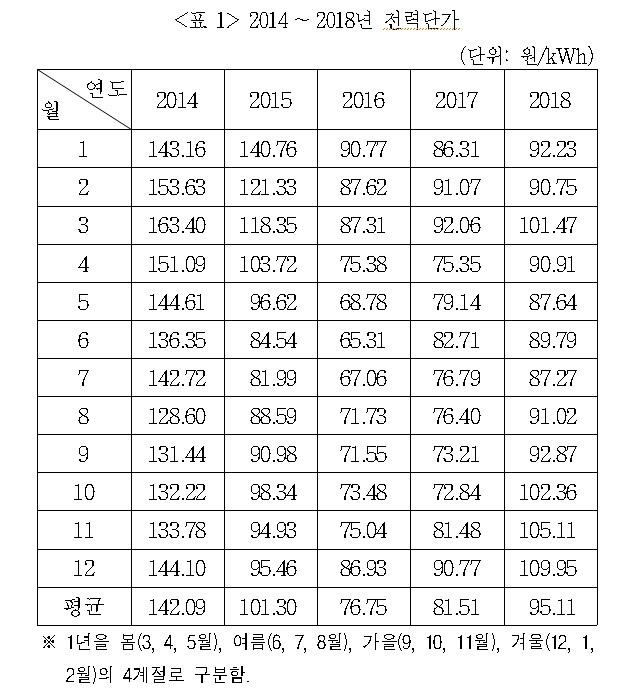

각주를 통해 여름과 가을이 속한 달을 알 수 있고 이를 헷갈리지 않도록 <표>에 표시해두도록 합시다. 그러면 여름은 6월∼8월, 가을은 9월∼12월이 되겠습니다. 해당 기간 동안의 전력단가 평균을 비교하는 선지입니다.
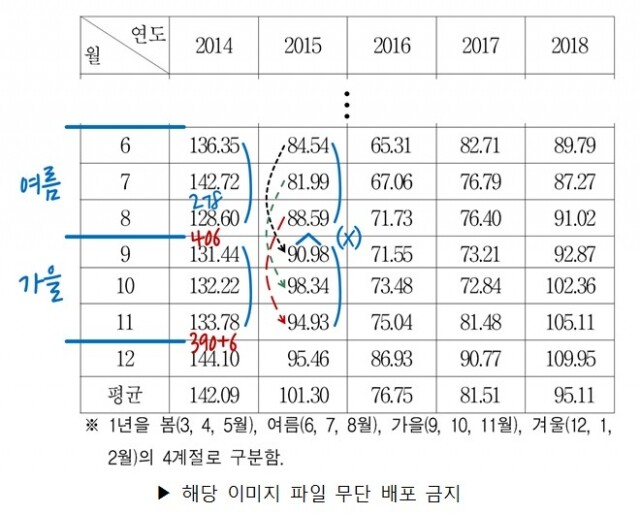
[개념을 활용한 계산 줄이기] 이때 이를 정확하게 계산하려면 각 기간에 속한 3개 전력단가를 모두 더해서 3으로 나누어 계산해야 하지만, 여름과 가을 모두 항목의 개수가 3개(3개월)로 동일하므로 평균비교는 3개 항목의 ‘합계 비교’를 통해 해결할 수 있습니다.
[필요한 계산은 효율적으로] 2014년부터 비교하면 가을(9∼11월)의 전력단가 합계(131+132+133)는 약 (130×3)+1+2+3=396 이고, 여름(6∼8월)의 3개월 전력단가 합계를 쉽표 앞자리만 구하면 약 406입니다. 그러므로 2014년은 여름의 합계가 더 높음을 알 수 있습니다.
[분포를 활용한 계산 줄이기] 2014년은 이처럼 효율적으로 계산한 반면, 2015년의 경우 계산 없이 간편하게 해결이 가능합니다. 6월(84)보다는 9월(90)이, 7월(81)보다는 10월(98)이, 8월(88)보다는 11월(94)이 더 값이 크기 때문에, ‘6월+7월+8월의 합(여름)’보다 ‘9월+10월+11월의 합(가을)’이 더 크다는 것을 수의 분포를 통해 알 수 있습니다. 따라서 언제나 여름의 평균값이 높다는 선지의 진술을 옳지 않은 진술이 됩니다.
이처럼 실전에서 순간순간 불필요한 계산은 줄이고 필요한 계산은 막힘없이 해결 갈 수 있다면 어려운 문제에서도 끊임없이 앞서갈 수 있게 될 것이고 반드시 성공하게 되어 있습니다. 만약 이 선지를 자신 있게 해결하지 못하고 계산을 어떻게 해야 할지 망설여지거나 시간이 지나치게 오래 걸렸다면 제 수업에 빠짐없이 담겨있는 실전 사고 기법들과 노하우들을 학습하시길 추천 드리고 싶습니다. 평소 계산과 관련된 고민들을 가벼이 여기지 마시고 속 시원하게 해결해 가시길 바랍니다. 감사합니다!!
[저작권자ⓒ 피앤피뉴스. 무단전재-재배포 금지]





























































